Using NetworkX to find all nodes/edges reachable from a given node and rank by path length

Find all of the nodes reachable from a given node

We can use shortest_path() to find all of the nodes reachable from a given node.

Alternatively, there is also descendants() that returns all nodes reachable from a given node (though the document [1] specified input G as directed acyclic graph.

First we create a sample graph (directed):

import networkx as net # version 2.5
import matplotlib.pyplot as plt
# Create a sample graph
g = net.DiGraph()
net.add_path(g, ['A','B','C'])
net.add_path(g, ['A','C','D'])
net.add_path(g, ['A','E','F'])

Plot it:

net.draw(g, with_labels=True, node_color='yellow')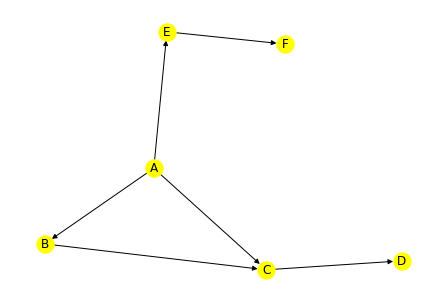

g_plot

To illustrate, we find all nodes connected to 'B' (the output will include 'B'):

nodes = net.shortest_path(g,'B').keys()
print(nodes)

Output:

dict_keys(['B', 'C', 'D'])

Alternatively, use descendants(G, source):

net.descendants(g, 'B')

Output:

{'C', 'D'}

Now let's see the undirected graph case:

u = g.to_undirected()
net.draw(u, with_labels=True, node_color='yellow')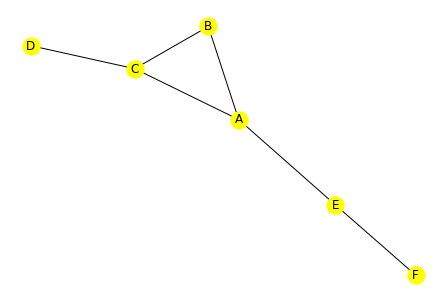

u_plot

We find all nodes connected to 'B' ('B' still in output):

# Get a list of nodes reachable from the given node 'B' (included).
nodes = net.shortest_path(u,'B').keys()
print(nodes)

Output:

dict_keys(['B', 'A', 'C', 'E', 'D', 'F'])

Find all of the edges reachable from the given node

We first create a subgraph containing all the reachable nodes found above:

  • Directed graph case:

      s = g.subgraph(nodes)
  print(s.edges())

    Output:

      OutEdgeView([('A', 'B'), ('A', 'C'), ('A', 'E'), ('B', 'C'), ('C', 'D'), ('E', 'F')])

    Or do it in one line:

      s = g.subgraph(net.shortest_path(g.to_undirected(),'B'))
  print(s.edges())

    Output:

      OutEdgeView([('A', 'B'), ('A', 'C'), ('A', 'E'), ('B', 'C'), ('C', 'D'), ('E', 'F')])

  • Undirected graph case:

      s = u.subgraph(nodes)
  s.edges()

    Output:

      EdgeView([('A', 'B'), ('A', 'C'), ('A', 'E'), ('B', 'C'), ('C', 'D'), ('E', 'F')])

Find the distance from a given node to all other nodes reachable (using undirected graph case as an example)

We can use shortest_path_length() to compute shortest path lengths in the graph and therefore calculating the distance.

# Specify both source and target
print(net.shortest_path_length(u, source = 'B', target = 'F'))
# Specify source
print(net.shortest_path_length(u, source = 'B'))
# Specify target
print(net.shortest_path_length(u, target = 'E'))
# Source,target not specified
P = dict(net.shortest_path_length(u))
P

Output:

3
{'B': 0, 'A': 1, 'C': 1, 'E': 2, 'D': 2, 'F': 3}
{'E': 0, 'A': 1, 'F': 1, 'C': 2, 'B': 2, 'D': 3}
{'A': {'A': 0, 'B': 1, 'C': 1, 'D': 2, 'E': 1, 'F': 2},
 'B': {'A': 1, 'B': 0, 'C': 1, 'D': 2, 'E': 2, 'F': 3},
 'C': {'A': 1, 'B': 1, 'C': 0, 'D': 1, 'E': 2, 'F': 3},
 'D': {'A': 2, 'B': 2, 'C': 1, 'D': 0, 'E': 3, 'F': 4},
 'E': {'A': 1, 'B': 2, 'C': 2, 'D': 3, 'E': 0, 'F': 1},
 'F': {'A': 2, 'B': 3, 'C': 3, 'D': 4, 'E': 1, 'F': 0}}

Reference